Kiến thức toán lớp 4 là nền tảng quan trọng để các em tiếp thu, học tập tốt toán lớp 5. Sau đây wikiso.net gửi đến phụ huynh và học sinh những kiến thức trọng tâm chương trình toán lớp 4, hệ thống các kiến thức toán cần nhớ để em tự tin học tốt toán ở các bậc học sau.
10 Kiến thức trọng tâm chương trình toán lớp 4 trọng tâm nhất!
1. Số tự nhiên
1.1 Số và chữ số
a) Dãy số tự nhiên
Các số 0, 1, 2, 3, …, 9, 10, …, 100, …, 1000, … là các số tự nhiên
Các số tự nhiên được sắp xếp theo thứ tự từ bé đến lớn tạo thành dãy số tự nhiên:
0,1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …
Các số tự nhiên có thể biểu diễn trên tia số:
Số 0 thì ứng với điểm gốc của tia số. Mỗi số tự nhiên ứng với 1 điểm trên tia số theo thứ tự tăng dần.
b)
Dùng 10 chữ số để viết số là 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Có 10 số có 1 chữ số (từ 0 đến 9)
Có 90 số có 2 chữ số (từ 10 đến 99)
Có 900 số có 3 chữ số (từ 100 đến 999)
Có 9000 số có 4 chữ số (từ 1000 đến 9999)
Số tự nhiên nhỏ nhất là số 0. Không có số tự nhiên lớn nhất
Hai số tự nhiên liên tiếp hơn hoặc kém nhau một đơn vị.
Không có số tự nhiên nào liền trước số 0 nên số 0 là số tự nhiên bé nhất.
Các số có chữ số tận cùng là 0, 2, 4, 6, 8 được gọi là số chẵn. Hai số chẵn liên tiếp hơn hoặc kém nhau 2 đơn vị
Các số có chữ số tận cùng là 1, 3, 5, 7, 8 được gọi là số lẻ. Hai số lẻ liên tiếp hơn hoặc kém nhau 2 đơn vị.
1.2 Hàng và lớp
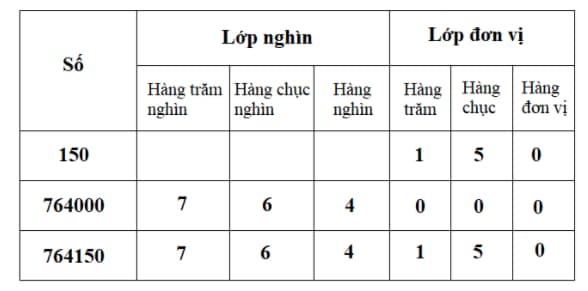
Hàng đơn trăm, hàng chục, hàng đơn vị hợp thành lớp đơn vị
Hàng trăm nghìn, hàng chục nghìn, hàng nghìn hợp thành lớp nghìn
Hàng triệu, chục triệu, trăm triệu hợp thành lớp triệu
1.3 Cách đọc số tự nhiên
Khi đọc số tự nhiên bạn cần đọc từ trái sang phải hay từ hàng cao đến hàng thấp.
Các chữ số từ phải sang trái lần lượt thuộc hàng đơn vị, hàng chục, hàng trăm, hàng nghìn, hàng chục nghìn, hàng trăm nghìn,…
1.4 Cách so sánh các số tự nhiên
Trong hai số tự nhiên:
Số nào có nhiều chữ số hơn thì số kia lớn hơn. Số nào có ít chữ số hơn thì bé hơn.
Nếu hai số có chữ số bằng nhau thì so sánh từng cặp số ở cùng 1 hàng.
Ví dụ như so sánh 157 và 175
157 < 175 vì: 1 = 1, 5 <7 nên suy ra 157 < 175
Nếu hai số có tất cả các cặp chữ số từng hàng đều bằng nhau thì hai số đó bằng nhau
1.5 Dãy số

2. Ôn tập các đại lượng chương trình toán lớp 4
2.1 Bảng đơn vị đo khối lượng
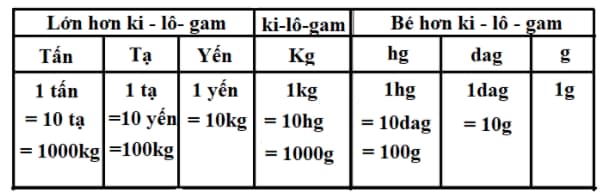
Để đo khối lượng các vật nặng hàng chục, hàng trăm, hàng nghìn, hàng ki-lo-gam thì chúng ta sử dụng đơn vị đo là: yến, ta, tấn
Để đo khối lượng các vật nặng hàng chục, hàng trăm, hàng nghìn gam người ta dùng những đơn vị như: đề-ca-gam, héc-tô-gam
Mỗi đơn vị đo khối lượng gấp 10 lần đơn vị bé liền sau nó. Ví dụ 1 yến = 10kg tức là 1 yến gấp 10 lần kg
Mỗi đơn vị đo khối lượng kém 1/10 lần đơn vị lớn hơn liền trước.
2.2. Bảng đơn vị đo độ dài
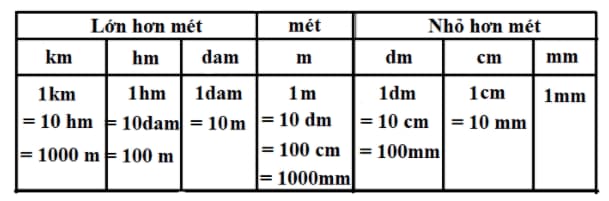
Đây là bảng đơn vị dùng để đo độ dài thực tế các vật, quãng đường, chiều cao,…
+) Mỗi đơn vị đo độ dài đều gấp 10 lần đơn vị bé hơn liền sau nó
+) Mỗi đơn vị đo độ dài đều kém 1/10 đơn vị lớn hơn liền trước nó
Để đo diện tích lớn như diện tích thành phố, chiều dài con đường,… người ta hay sử dụng đơn vị đo là ki-lô-mét-vuông
- Ki lô mét vuông là diện tích hình vuông có chiều dài cạnh là 1km
- Ki-lô-mét vuông được viết tắt là km2
- Đơn vị đo diện tích kí hiệu là: km2, m2, dm2, cm2
1km2 = 1 000 000m2
1m2 = 100dm2
1m2 = 10 000cm2
1dm2 = 100cm2
2.3 Đơn vị đo thời gian (giây – thế kỷ)
Ta có các quy ước như sau:
1 giờ = 60 phút
1 phút = 60 giây
1 năm = 12 tháng
1 năm không nhuận = 365 ngày
1 năm nhuận = 366 ngày
1 thế kỷ = 100 năm
Có từ năm 1 đến năm 100 là thế kỷ một (thế kỷ I)
Từ năm 101 đến năm 200 là thế kỷ hai (thế kỷ II)
Từ năm 201 đến năm 300 là thế kỷ ba (thế kỷ III)
…
Từ năm 1901 đến năm 2000 là thế kỷ hai mươi (thế kỷ XX)
Từ năm 2001 đến năm 2100 là thế kỷ hai mươi mốt (thế kỷ XXI)
Đặc biệt chú ý:
Các tháng 1, 3, 5, 7, 8, 10, 12 có 31 ngày
Tháng 4, 6, 9, 11 có 30 ngày
Tháng 2 có 28 ngày (năm nhuận là 29 ngày)
3. Ôn tập về phân số và các phép tính phân số
3.1 Khái niệm phân số


3.2 Tính chất cơ bản của phân số
Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Nếu chia cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho
3.3 So sánh các phân số
a) Cách so sánh các phân số cùng mẫu số
Trong hai phân số có cùng mẫu số ta so sánh như sau:
+ Phân số nào có tử số bé hơn thì phân số đó bé hơn
+ Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
+ Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
b) So sánh các phân số cùng tử số
Trong hai phân số có cùng tử số thì ta cần làm như sau:
+ Phân số nào có mẫu số bé hơn thì phân số đó lớn hơn
+ Phân số nào có mẫu số lớn hơn thì phân số đó bé hơn.
+ Nếu mẫu số bằng nhau thì hai phân số đó bằng nhau.
c) Cách so sánh các phân số khác mẫu.
Nếu muốn so sánh hai phân số khác mẫu số, ta có thể đông quy mẫu số hai phân số đó rồi so sánh các tử số của hai phân số mới
3.4 Các phép tính phân số
a) Phép cộng phân số
Để cộng hai phân số có cùng mẫu số, ta cộng hai tử số với nhau và giữ nguyên mẫu số
Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số rồi cộng hai phân số với nhau.
b) Phép trừ phân số
Muốn trừ hai phân số có cùng mẫu ta làm như sau: trừ tử số của phân số thứ nhất cho tử số của phân số thứ 2, giữ nguyên mẫu số ta được kết quả của phép trừ hai phân số cùng mẫu.
Muốn trừ hai phân số khác mẫu ta làm như sau: đưa mẫu của 2 phân số về mẫu chung nhất bằng cách quy đồng mẫu số hai phân số rồi đưa về cách trừ hai phân số có cùng mẫu số.
c) Phép nhân phân số
Muốn nhân hai phân số với nhau ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
d) Phép chia phân số
Muốn chia một phân số cho một phân số ta lấy tử số của phân số thứ 1 nhân với mẫu số của phân số thứ 2, mẫu số của phân số thứ nhất nhân với tử số của phân số thứ 2.
4. Số trung bình cộng
4.1 Các bài toán tìm số trung bình cộng
Một vài kiến thức cần nhớ
- Muốn tìm số trung bình cộng của nhiều số, ta tính tổng của các số đó, rồi lấy tổng đó chia cho số các số hạng.
Ví dụ: Tìm trung bình cộng của 18, 19, 23 là
(18 + 19 + 23) : 3 = 20
- Số trung bình cộng của dãy cách đều : (số đầu + số cuối) : 2
4.2 Bài toán: tìm số hạng khi biết trung bình cộng và số hạng khác
a) Trung bình cộng của dãy số cách đều
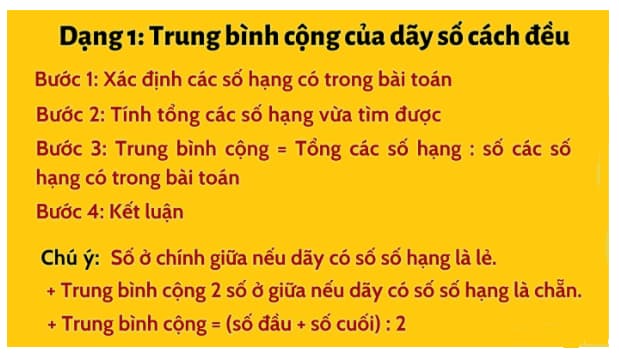
b) Sử dụng sơ đồ để giải bài toán trung bình cộng

5. Dạng toán tìm hai số khi biết tổng và hiệu

6. Dạng toán tìm hai số khi biết tổng – tỉ hoặc hiệu – tỉ của hai số đó
6.1 Tìm hai số khi biết tổng và tỉ

6.2 Tìm hai số khi biết hiệu và tỉ

7. Ôn tập về phép nhân, chia, cộng, trừ và các dạng toán đặt tính
7.1. Các phép tính số tự nhiên chương trình toán lớp 4
a) Phép nhân
Tính chất giao hoán: a x b = b x a
Tính chất kết hợp: a x (b x c) = (a x b) x c
Nhân với số 0: a x 0 = 0 x a = 0
Nhân với số 1: a x 1 = 1 x a = a
Nhân một số với một tổng: a x (b + c) = a x b + a x c
Khi nhân một số với một tổng, ta có thể nhân số đối với từng số hạng của tổng rồi cộng kết quá với nhau
Nhân một số với một hiệu: a x (b – c) = a x b – a x c
Khi nhân một số với một hiệu, ta có thể lần lượt nhân số đó với một số bị trừ và số trừ rồi trừ hai kết quả cho nhau.
Chú ý:
Trong một tích nếu thừa số được gấp lên n lần đồng thời có một thừa số khác bị giảm đi n lần thì tích không đổi
Ở một tích nếu thừa số được gấp lên n lần và các thừa số còn lại giữ nguyên thì tích được gấp lên n lần và ngược lại. Trong một tích có một thừa số bị giảm đi n lần thì các thừa số còn lại giữ nguyên thì tích cũng bị giảm đi n lần (điều kiện: n > 0)
Một tích, nếu có ít nhất một thừa số chẵn thì sẽ cho kết quả tích chẵn.
Trong một tích, nếu thừa số được tăng thêm a đơn vị các thừa số còn lại giữ nguyên thì tích được thêm a lần tích các thừa số còn lại.
Trong một tích các thừa số đều lẻ và có ít nhất 1 thừa số có tận cùng là 5 thì tích có tận cùng là 5.
b) Phép chia
Một số chia cho một tích a : (b x c) = a : b : c (a,b > 0)
Một tích chia cho một số: (a x b) : c = (a : c) x b = a x (b : c)
Một số chia cho một thương a : (b : c) = a : b x c
Một tổng chia cho một số: (a + b) : c = a : c + b : c (c > 0)
Một hiệu chia cho một số: (a – b) : c = a : c – b : c (c > 0)
Chú ý
Trong phép chia, nếu số bị chia tăng hoặc giảm đi n lần (n > 0) và số chia giữ nguyên thì thương cũng tăng lên hoặc giảm đi n lần.
Trong phép chia thì nếu tăng số chia lên n lần (n > 0) đồng thời số bị chia được giữ nguyên thì thương giảm đi n lần và ngược lại.
Trong một phép chia, số chia và số bị chia cùng tăng hoặc giảm n lần thì thương không đổi
Một phép chia có dư, nếu số bị chia và số chia cùng được gấp hoặc giảm n lần (n > 0) thì số dư cũng được gấp (giảm) n lần
c) Phép cộng
Tính chất giao hoán: a + b = b + a
Tính chất kết hợp: a + b + c = (a + b) + c = a + (b + c) = b + (a + c)
a + 0 = 0 + a = a
(a – n) + (b + n) = a + b
(a – n) + (b – n) = a + b – n x 2
(a + n) + (b + n) = a + b + n x 2
Nếu một số hạng được gấp lên n lần đồng thời các số hạng còn lại được giữ nguyên thì tổng đó được tăng lên một số đúng bằng (n – 1) lần số hạng được gấp lên.
Nếu số hạng bị giảm đi n lần, đồng thời các số hạng còn lại được giữ nguyên thì tổng đó bị giảm đi một số đúng bằng ( 1 – ) số hạng bị giảm đi.
Tổng của các số chẵn là một số chẵn
Tổng của một số lẻ và một số chẵn là một số lẻ
Tổng của hai số tự nhiên liên tiếp là một số lẻ.
d) Phép trừ
a – (b + c) = (a – c) – b = (a – b) – c
Nếu số bị trừ và số trừ cùng tăng hoặc giảm n đơn vị thì hiệu của chúng không đổi
Nếu số bị trừ được gấp lên n lần và giữ nguyên số trừ thì hiệu được tăng thêm một số đúng bằng (n – 1) lần số bị trừ
Nếu số bị trừ giữ nguyên, số trừ được gấp lên n lần thì hiệu bị giảm đi (n – 1) lần số trừ
Nếu số bị trừ được tăng thêm n đơn vị, số trừ giữ nguyên thì hiệu giảm đi n đơn vị
7.2 Dạng toán đặt tính của phép cộng, trừ, nhân, chia kiến thức toán lớp 4
Phép nhân
- Khi thực hiện phép tính ta thực hiện từ phải qua trái
- Ta lần lượt có các tích riêng thứ 1, 2, 3… khi đặt tính nhớ phải đặt thẳng hàng các chữ số
Phép chia
- Thực hiện phép tính theo thứ tự từ trái qua phải.
- Có đủ 3 phép tính trong phép chia gồm: Chia sau đó nhân rồi cuối cùng trừ.
- Trong phép chia có dư thì số dư bao giờ cũng nhỏ hơn số chia.
Phép cộng
Quy tắc: Muốn cộng hai số tự nhiên ta có thể làm như sau:
- Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
- Cộng các chữ số ở từng hàng theo thứ tự từ phải sang trái, tức là từ hàng đơn vị đến hàng chục, hàng trăm, hàng nghìn, … .
Phép trừ
Quy tắc: Muốn trừ hai số tự nhiên ta có thể làm như sau:
- Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
- Trừ các chữ số ở từng hàng theo thứ tự từ phải sang trái, tức là từ hàng đơn vị đến hàng chục, hàng trăm, hàng nghìn, …
8. Tỉ lệ bản đồ và ứng dụng của tỉ lệ bản đồ
Khi bạn nhìn ở phần bản đồ tỉnh, thành phố, quốc gia, trái đất bạn thấy có ghi: tỉ lệ 1 : 10 000 000. Thì nó chính là tỉ lệ bản đồ
Tỉ lệ 1 : 10 000 000 hay 1/10 000 000 có nghĩa là tỉ lệ về quốc gia, tình thành được vẽ thu nhỏ lại tới 10 000 000 lần.
Ứng dụng của tỉ lệ bản đồ
Tính độ dài thật
Tính độ dài thu nhỏ trên bản đồ.
9. Dấu hiệu chia hết cho 2, 5, 3, 9 kiến thức trọng tâm chương trình toán lớp 4
9.1 Dấu hiệu chia hết cho 2
Các số có chữ số có tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2. Số chia hết cho 2 là số chẵn
Ví dụ:
10 : 2 = 5
16 : 2 = 8
38 : 2 = 19
9.2 Dấu hiệu chia hết cho 3
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3. Tổng các chữ số không chia hết cho 3 thì không chia hết cho 3.
Ví dụ:
33 : 3 = 11
Ta có:
3 + 3 = 6
6 : 3 = 2
9.3 Dấu hiệu chia hết cho 5
Các số có tận cùng là 0 hoặc 5 thì đều chia hết cho 5
Các số không có chữ số tận cùng là 0 hoặc 5 thì không chia hết cho 5
Các số có chữ số tận cùng là 0 thì chia hết cho cả 2 và 5.
Ví dụ:
40 : 5 = 8
35 : 5 = 7
9.4 Dấu hiệu chia hết cho 9
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9. Các số có tổng các chữ số không chia hết cho 9 thì không chia hết cho 9.
Ví dụ:
81 : 9 = 9
Vì 8 + 1 = 9, 9 : 9 = 1 nên suy ra 81 chia hết cho 9.
10. Ôn tập về hình học kiến thức trọng tâm chương trình toán lớp 4
10.1 Hình chữ nhật
+ Nếu tăng chiều dài của hình chữ nhật lên a đơn vị thì chu vi sẽ tăng lên a x 2
+ Nếu tăng chiều rộng của hình chữ nhật lên a đơn vị thì chu vi sẽ tăng lên a x 2
+ Nếu giảm chiều dài của hình chữ nhật lên a đơn vị thì chu vi sẽ giảm lên a x 2 đơn vị
+ Nếu giảm chiều rộng của hình chữ nhật lên a đơn vị thì chu vi sẽ giảm lên a x 2 đơn vị
+ Nếu gấp 1 chiều nào đó của hình chữ nhật lên bao nhiêu lần thì diện tích sẽ tăng lên bấy nhiêu lần.
+ Nếu giảm 1 chiều nào đó của hình chữ nhật lên bao nhiêu lần thì diện tích sẽ giảm đi số lần
+ Trong hình vuông, nếu tăng 1 cạnh lên a đơn vị thì chu vi sẽ tăng lên 4 x a đơn vị
+ Trong hình vuông nếu cạnh tăng lên a lần thì diện tích tăng lên a x a lần
10.2 Hình bình hành và diện tích hình bình hành
a) Hình bình hành
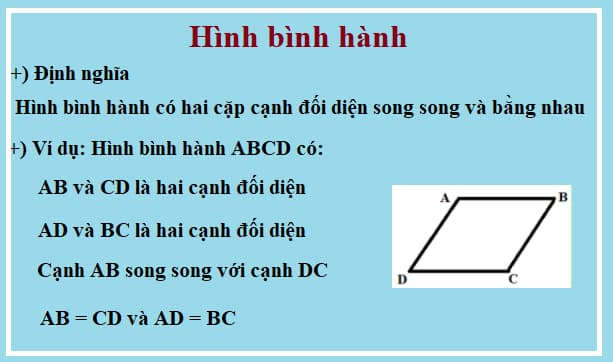
b) Diện tích hình bình hành
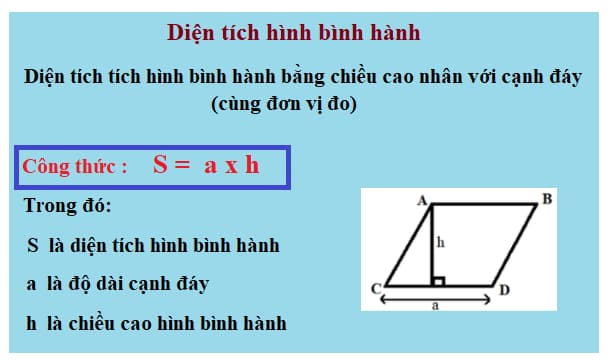
10.3. Hình thoi và diện tích hình thoi
a) Hình thoi

b) Diện tích hình thoi
Cho hình thoi ABCD có AC = m, BD = n
Cắt hình tam giác AOD và hình tam giác COD ghép với hình tam giác ABC để được hình chữ nhật MNCA như hình vẽ.
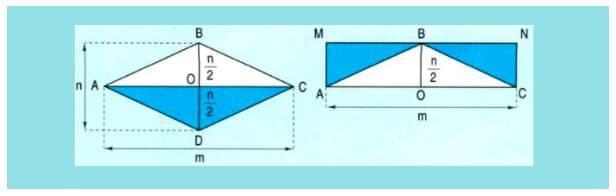
Dựa vào hình vẽ ta có:
Diện tích hình thoi ABCD bằng diện tích hình chữ nhật MNCA
Diện tích hình chữ nhật MNCA là:
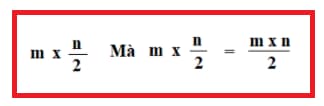
Vậy diện tích hình thoi ABCD là: (m x n) : 2
Diện tích hình thoi bằng tích của độ dài hai đường chéo chia cho 2 (cùng đơn vị đo):

Trong đó: S là diện tích hình thoi; m, n là độ dài của hai đường chéo
10.4 Hai đường thẳng vuông góc

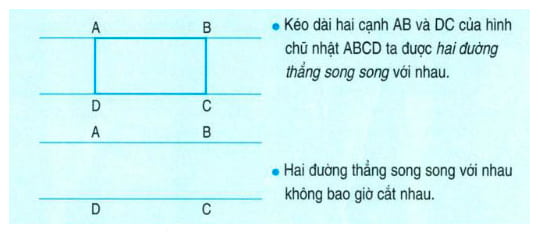
10.5 Hai đường thẳng song song
Như vậy wikiso đã giới thiệu tới phụ huynh, học sinh 10 kiến thức trọng tâm chương trình toán lớp 4 quan trọng nhất, con cần ghi nhớ chăm chỉ luyện bài tập để củng cố kiến thức. Để con say mê học toán hơn, cha mẹ nên dành thời gian đồng hành cùng con nhé! Chúc con học tốt đạt kết quả cao













